Article #2: Specific Speed
(NS) - Why Is It Dimensionless, or - Is It?
Pump Specific Speed
is one of the several dimensionless parameters used in pumps. Pump designers
like to use dimensionless numbers, because his allows them to analyze and compare
pump performance regardless of size.
Otherwise, how would
you compare a 6" pump performance with a 10" pump?
What is a typical
maximum efficiency is to be expected from a given pump? There is an infinite
variation of pump sizes, flows, generated pressures, speeds, etc.- so, it would
be impossible to compare a performance of the 6" pump running at 3200 rpm
at 200 gpm, with a 10” pump running at 1400 rpm at, say, 310 gpm.
Besides, the same
performance can be achieved by a wider impeller with a narrower volute, as by
the narrower impeller with a wider volute, if their outside diameters are
different. In other words, there is an infinite variation of operating
parameters (flows, heads, speeds) that depend on an infinite variation of pump
geometry internals.
A specific speed NS
reduces this infinite variation of performance parameters into a single number,
and an infinite variation of geometries into a single characteristic
non-dimensional impeller profile shape. Then, a given impeller shape would point
at the unique performance factor, i.e. specific speed.
Obviously, to
eliminate dependency of the operating parameters specific speed must be
dimensionless, otherwise the remaining dimension (gallons, pounds, feet, etc.)
would affect the comparison. Originally, specific speed was defined as:
OmegaS = Rotating Speed x Flow0.5 / Head0.75
,
The units had to be
in any system of "consistent" units, for example:
Rotational Speed - 1/sec
Flow
- ft3/sec,
Head in feet times the gravitational
constant (which has units of ft/sec2):
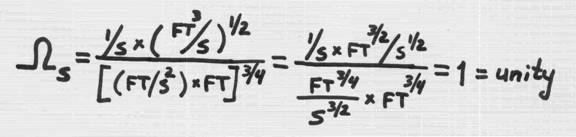
This is how the
initial definition of "specific speed" was meant to be
"dimensionless". But, such set of units is awkward, and the
gravitational constant is simply dropped, and flow is entered in gpm, and
rotational speed in RPM.
Specific speed thus
defined is denoted NS. Strictly speaking, such modified definition is not
dimensionless, but the proportionality terms are constants (such as ft3/sec
x 448.8 = gpm), which makes the NS directly proportional to "OmegaS".
The non-dimensional nature of the NS (disregarding the dropped constant) makes
it independent of rotational speed RPM. This is because of the affinity laws
governing the operation of the centrifugal pump. These state that flow varies
linear with speed, and head as a square:
Q
~ RPM
H
~ RPM2
If RPM is changed
n-times, flow changes n-times also, and head changes n2 times.
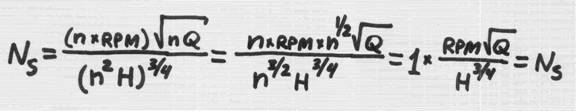
(Note that NS has not changed when
RPM changed).
Incidentally, similar
rule happen to apply to impeller OD cut: if impeller diameter changes n-times:
flow changes linearly, and head as a square. The net result: no change in NS.
Also, if all geometric linear dimensions of a pump are changed at the same
ratio, its specific speed still remains constant. (This part, however, is more specialized, - usually of the realm of
the pump hydraulics designers - see special discussion on that):
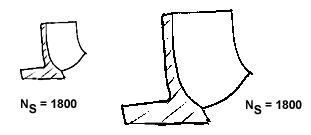
Same shape,
but different size – i.e. Specific Speed is a measure of the impeller
geometry similarity (i.e. “affinity”), - not the size of it. In other words, if
you are looking at a cross-sectional drawing of a pump, there would be a
certain specific speed NS, unique to the impeller shape - regardless whether
you are looking at a cross-section of a 6" design, or a 60" design.
It was discovered
that a pump efficiency at the best efficiency point (BEP) depends mainly on the
Specific Speed, and a pump with Specific Speed of 1500 is more efficient then
the one with specific speed of 1000. Charts and publications were developed,
and are available as an estimate of a "reasonably achievable"
efficiency for a given pump, versus actual.
Similarly to pump
specific speed (NS), a concept of a suction specific speed (NSS) has also been
introduced. Here, the head at the denominator is substituted by the NPSHR at
the BEP. But this is a separate discussion (see among other Articles).
To
learn more about this topic, e-mail your comments to us at: